Digitalisierung
Klaus von der Heide
Mikrofon
Die durch Fledermausrufe verursachten Schalldruckschwingungen werden mit einem Mikrofon in Spannungsschwingungen gewandelt. Die bewegliche Membran im Mikrofon muss kleiner sein als die Hälfte der kleinsten aufzunehmenden Wellenlänge. Die Wellenlänge ist bei einer Frequenz von 180 kHz nur knapp 2 mm. Bei solchen Frequenzen sollten die Durchmesser der Membranen kleiner als 1 mm sein, andernfalls ergeben sich Richtcharakteristiken mit mehreren Keulen und Nullstellen.
Mikrofonverstärker
Die vom Mikrofon abgegebene sehr kleine Spannung muss mit einem analogen Verstärker in den Spannungsbereich transformiert werden, der vom nachfolgenden Analog-Digital-Wandler benötigt wird, z.B. -1 V bis +1V. Üblicherweise gleicht dieser Verstärker eine Frequenz-abhängige Empfindlichkeit des Mikrofons aus. Die Verstärkung sollte einstellbar sein, um den vom A/D-Wandler benötigten Spannungsbereich voll auszunutzen ohne ihn zu überschreiten.
Digitalisierung
Ziel der Digitalisierung ist, das in der Zeit kontinuierlich ablaufende Spannungssignal mit auch in der Spannung kontinuierlichen Spannungswerten umzuwandeln in eine Zeit-diskrete Sequenz von Binärzahlen, welche die zu den diskreten Zeiten abgetasteten Spannungswerte repräsentieren. Die Digitalisierung betrachten wir in zwei Schritten: zunächst die Zeit-Diskretisierung und anschließend die Wert-Diskretisierung.
Zeit-Diskretisierung
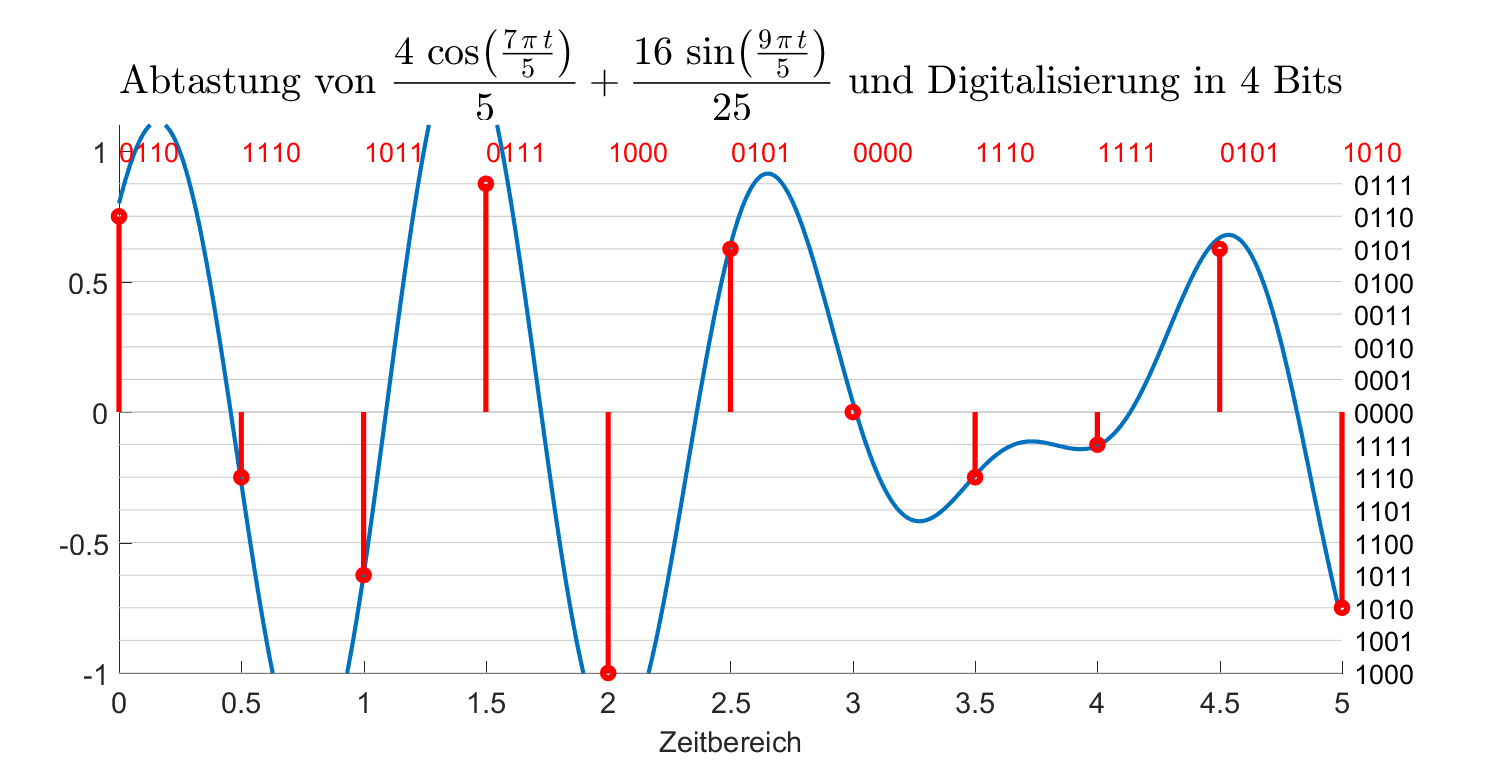
Anstelle der kontinuierlichen Zeit wird ein äquidistentes Zeitraster durch eine Abtastrate definiert. Die Abtastrate gibt an, wieviele Abtastungen pro Zeiteinheit vorzunehmen sind. Das nachfolgende Beispiel zeigt eine Abtastung mit der Abtastrate 16/Zeiteinheit.
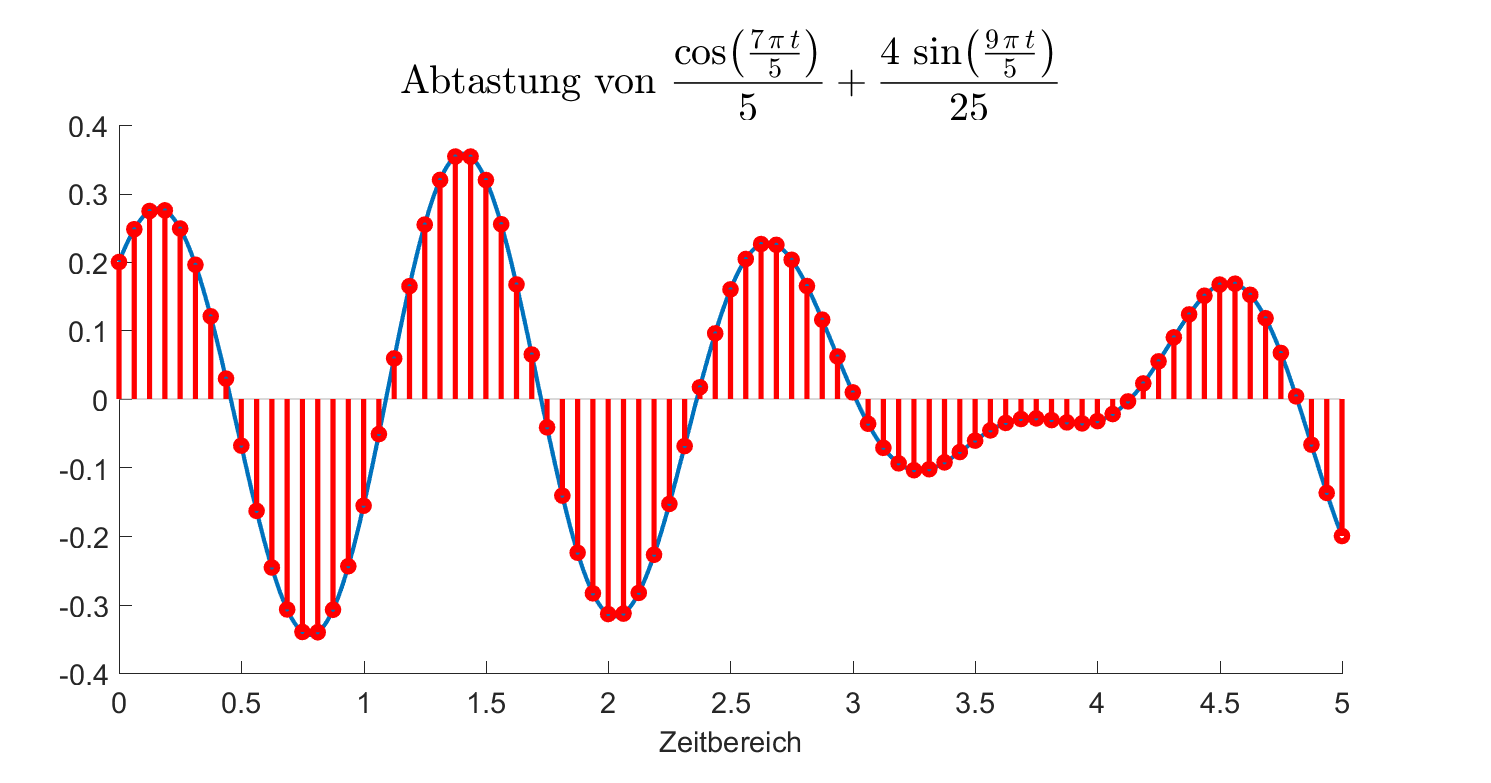
Die roten Punkte zeigen die abgetasteten Werte, die hier noch nicht digitalisiert sind.
Die wichtigste Frage bei der Zeit-Diskretisierung ist die nach der angemessenen Abtastrate. Sie wurde 1933 durch Kotelnikow mathematisch beantwortet. Allerdings wird das Resultat meist als Nyquist-Theorem bezeichnet. Es besagt, dass die Abtastrate wenigstens das doppelte der Breite des durch das Signal belegten Frequenzbandes sein muss (sog. Nyquist-Frequenz). Im vorliegenden Fall, wo die höchste vorkommende Frequenz (im sin) 0.9/Zeiteinheit beträgt, ergibt sich als minimale Abtastrate 1.8/Zeiteinheit. Das folgende Bild zeigt eine Abtastung mit der Rate 2/Zeiteinheit. Da diese Abtastrate größer als die Nyquist-Frequenz ist, enthalten die abgetasteten Werte alle Information, um jeden Punkt der Zeit-kontinuierlichen Funktion nach Bedarf rekonstruieren zu können.
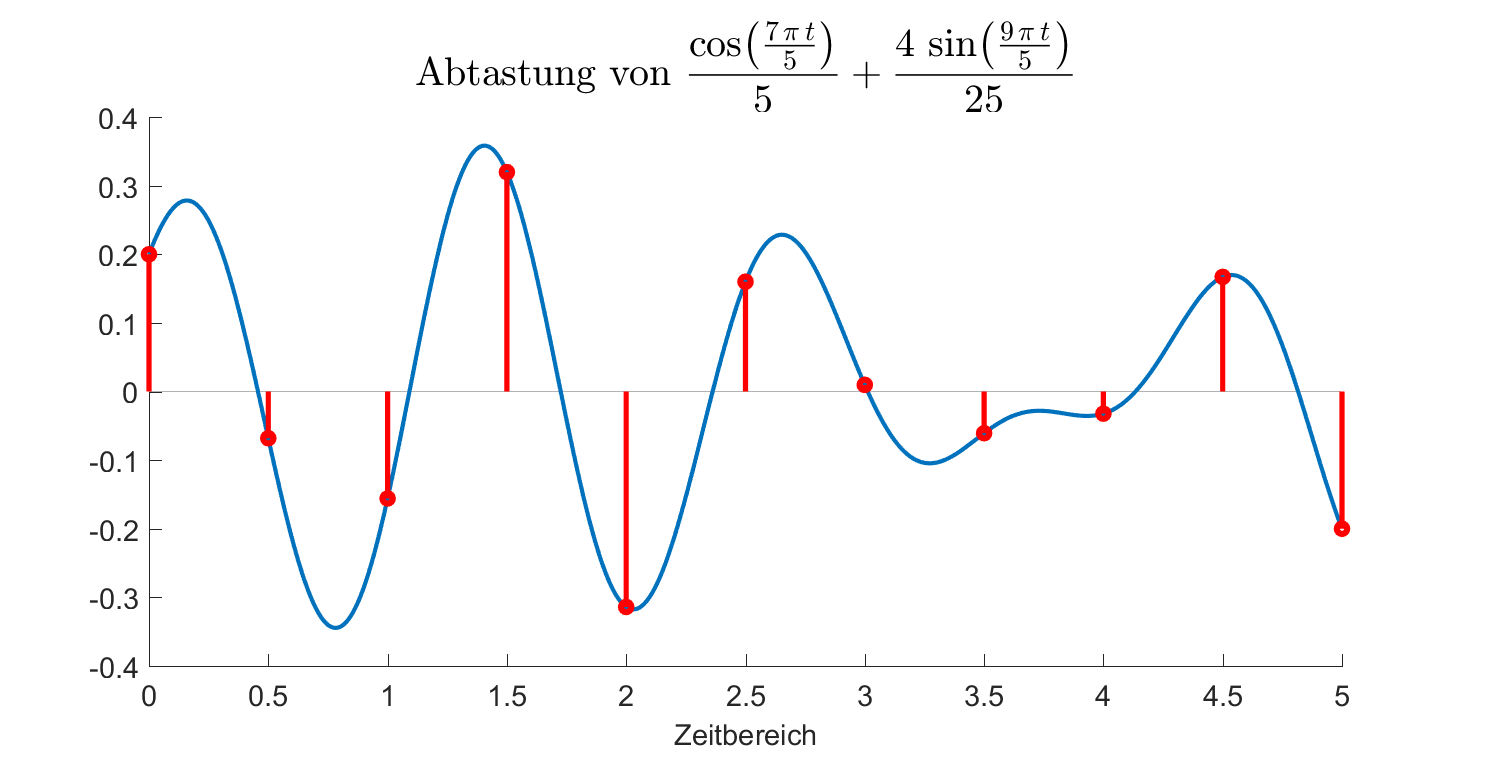
Rekonstruktion des Zeit-kontinuierlichen Signals
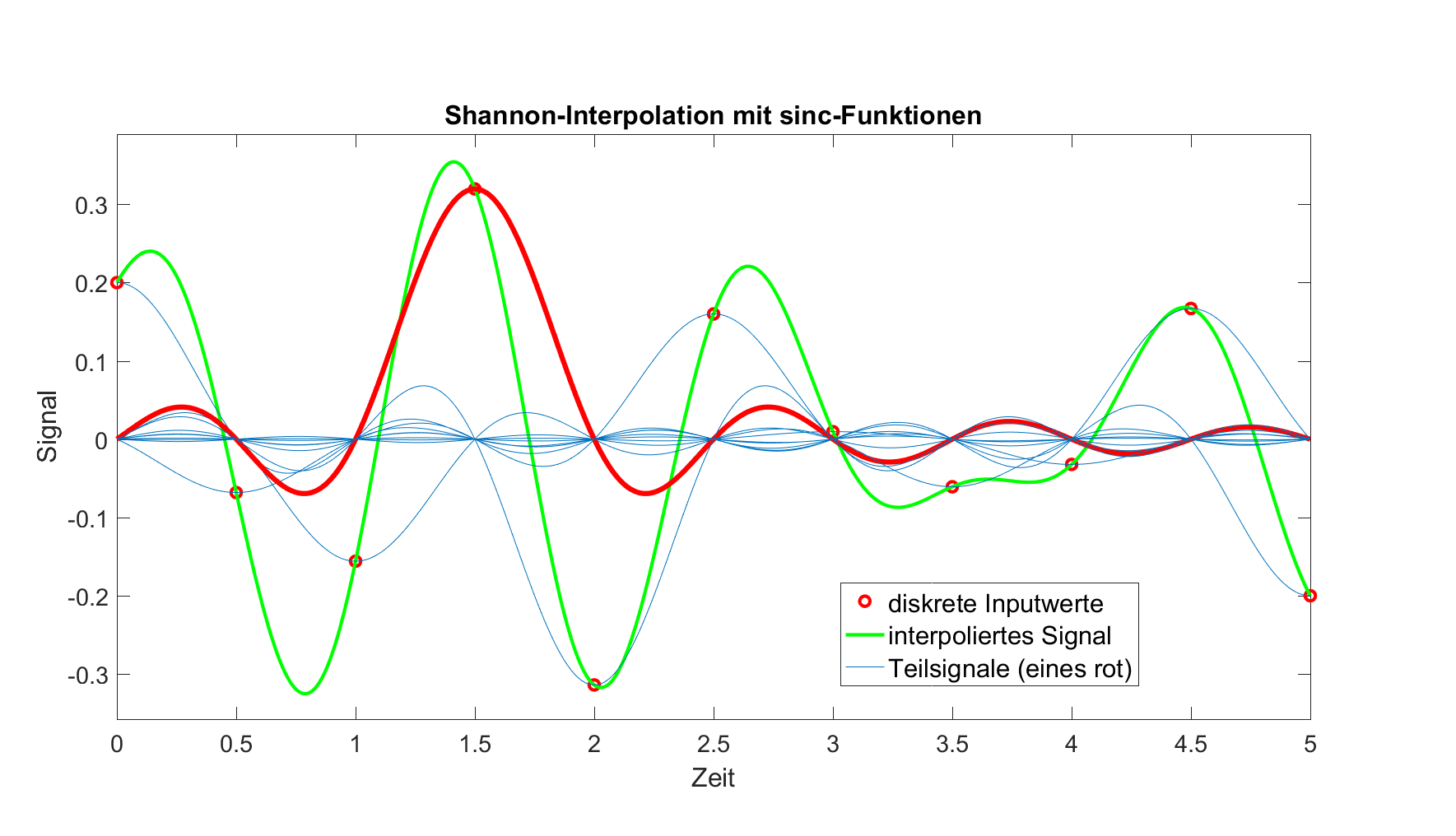
Die Rekonstruktion erfolgt nach Shannon dadurch, dass durch jeden Abtastwert eine sinc-Funktion gelegt wird. Diese ist nachfolgend dargestellt.

Für das Abtastbeispiel mit 11 Abtastpunkten ergibt das 11
sinc-Funktionen, die alle zu addieren sind. Die sinc-Funktion der vierten
Abtastung ist zur Verdeutlichung in rot dargestellt, die Summe aller
sinc-Funktionen in grün.
Voraussetzung für das Abtasttheorem
Die Summe (grün) sollte dem oben im Beispiel blau dargestellten Signalverlauf exakt gleichen. Das ist aber nicht der Fall, weil in diesem Beispiel nur 11 Abtastungen aus dem im Prinzip unendlich langen Signal herausgeschnitten wurden. Damit fehlen alle außerhalb des Zeitfensters liegenden sinc-Funktionen. Die Rekonstruktion - und damit auch das Abtasttheorem - gehen von in beiden Zeitrichtungen unendlich langen Signalen aus. Jedes in der Praxis vorkommende Signal ist aber endlich. Den dadurch unvermeidlichen Rekonstruktionsfehler kann man beliebig klein machen durch Anfügen von geeigneten Signalstücken an Anfang und Ende des interessierenden Signals und passende Fensterung, auf die wir später zurückkommen.
Wenn man andererseits einfach annimmt, dass das Signal in unserem Beispiel vor der Zeit 0 und nach der Zeit 5 durchweg Null ist, dann sind auch alle dort eingefügten sinc-Funktionen Null. Damit ist das Signal nun künstlich unendlich lang und die Rekonstruktion ist vollständig. Dennoch ist die Nyquist-Bedingung verletzt, denn das kurze Signal enthält nun die unstetigen Signalsprünge bei 0 und 5. Diese haben Frequenzanteile zur Folge, die weit oberhalb der angenommenen Nyquist-Frequenz liegen.
Wert-Diskretisierung
Nachdem die Zeit-diskreten Abtastwerte vorliegen, müssen diese jetzt digitalisiert werden. Dazu wird der Spannungsbereich gerastert in ein Gitter mit 2n Rasterlinien. Jeder Rasterlinie wird eine Binärzal mit n Bit zugeordnet (schwarze Binärzahlen am rechten Rand des folgenden Bildes). Als digitale Repräsentation des Abtastwertes wird die Binärzal genommen, die der nächstliegenden Rasterlinie zugeordnet ist. Diese digitalen Abtastungen sind im Bild oben in rot angegeben.