Ultraschall-Akustik
Klaus von der Heide
Schallwellen mit Frequenzen oberhalb des menschlichen Hörbereichs, der bis zu 20 kHz reichen kann, werden als Ultraschallwellen bezeichnet. Ihre Ausbreitung in Luft und die Reflexion an Flächen werden durch dieselben physikalischen Gesetze beschrieben wie die des normalen Schalls. Wenn man also die Wellenlänge um einen Faktor w verringert und ebenso sämtliche Abmessungen eines Versuchsaufbaus, so ergibt sich bis auf nichtlineare Effekte der Schallausbreitung dasselbe. Die übliche Situation ist allerdings eine andere: Man bleibt bei denselben räumlichen Gegebenheiten und testet die Akustik bei sehr unterschiedlichen Frequenzen. Drei offensichtliche Effekte werden nachfolgnd beschrieben.
Schallgeschwindigkeit
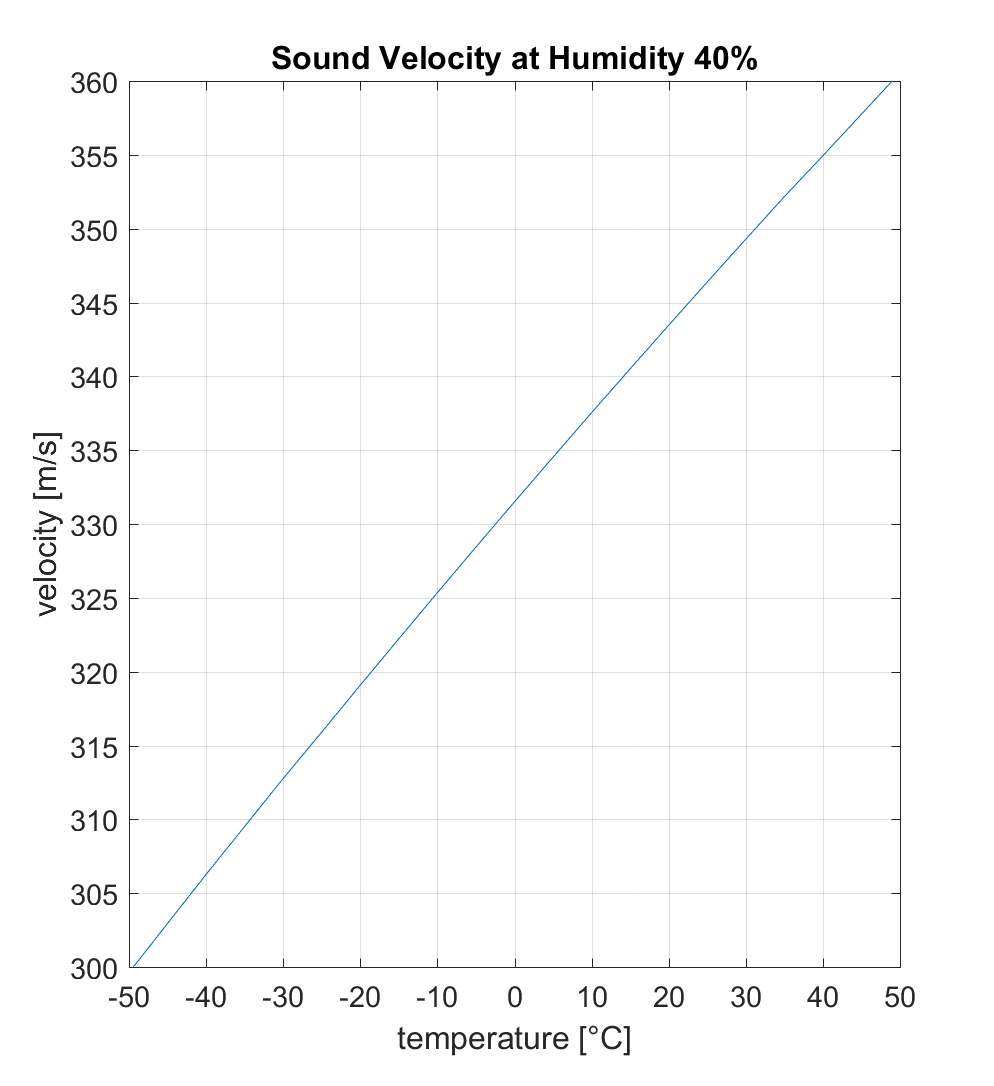
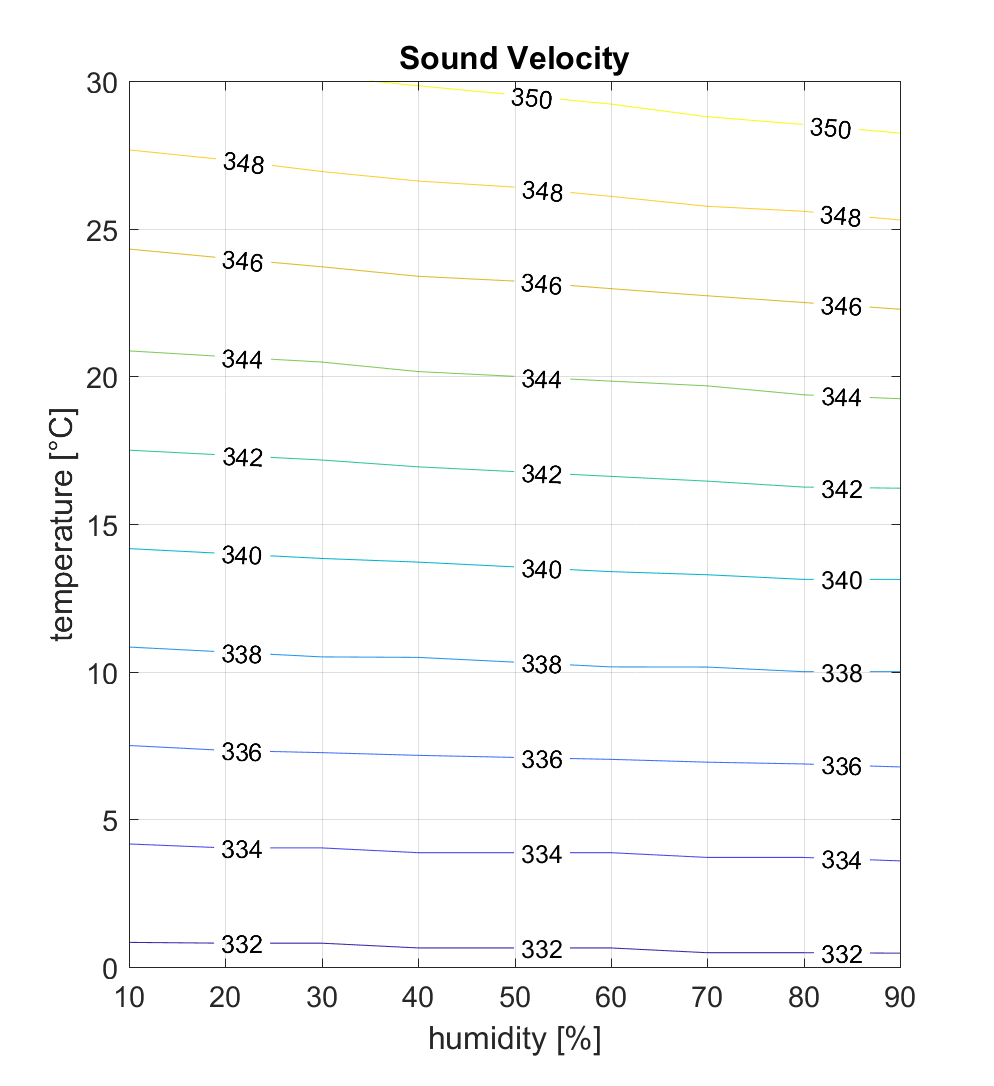
Die Schallgeschwindigkeit hängt von der Temperatur und der Luftfeuchtigkeit ab. Dies zeigen zwei Graphiken:
Schalldämpfung
Ohne irgendwelche Dämpfung bei der Ausbreitung wäre die Amplitude einer vom Mikrofon aufgenommenen Schwingung umgekehrt proportional zur Entfernung des Mikrofons von der Schallquelle. Dieses Gesetz ist unabhängig von der Frequenz. Wir wollen nachfolgend nur die noch hinzukommende Dämpfung als Faktor betrachten.
Die Dämpfung von Schallwellen ist stark abhängig von ihrer Frequenz. Das folgende Bild zeigt die Dämpfung als Faktor über der Frequenz mit der Distanz D zwischen Schallquelle und Mikrofon als Parameter. Die Dämpfung ist auch abhängig von der Luftfeuchtigkeit, jedoch kaum von der Temperatur.
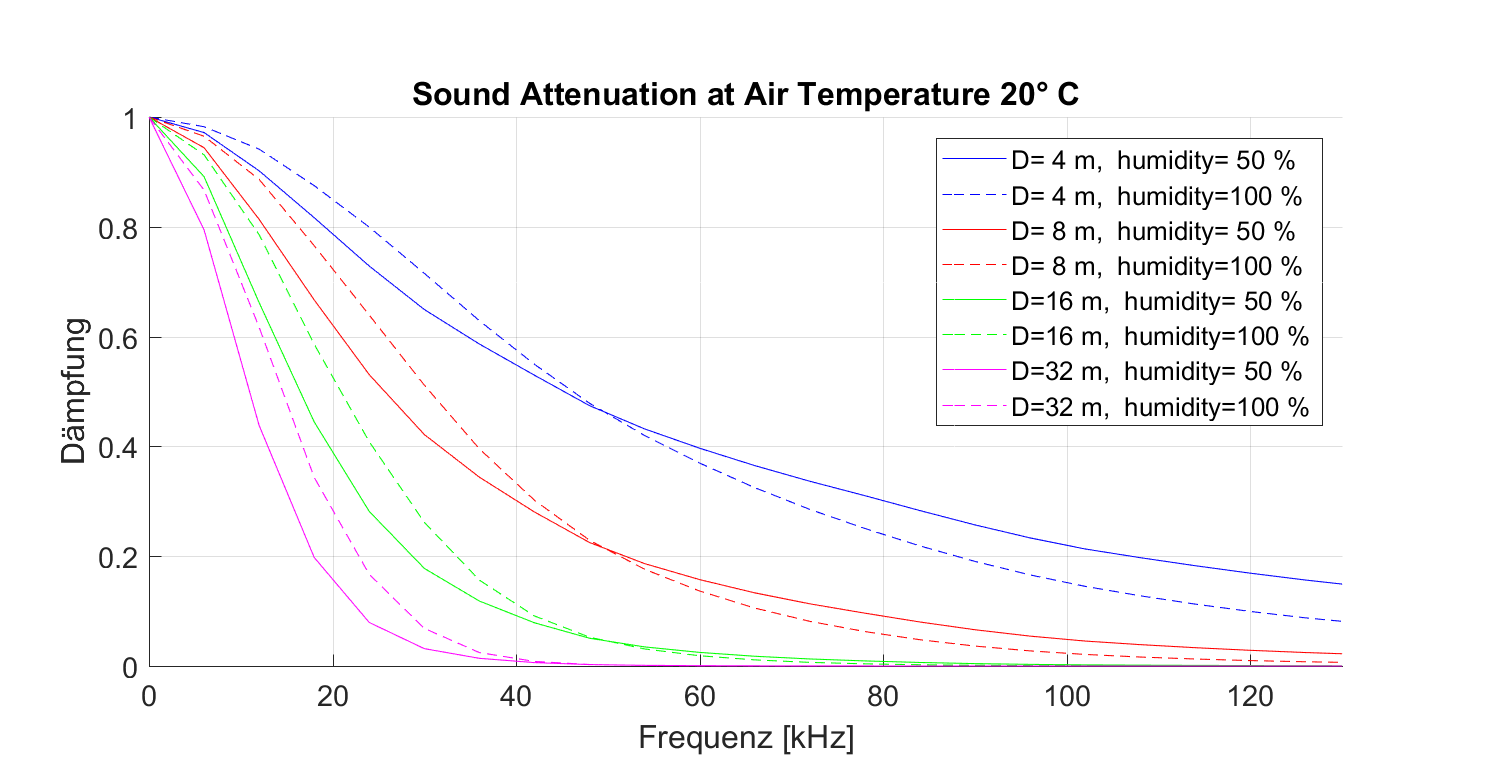
Dieses Bild macht deutlich, warum kleine Hufeisennasen mit ihrer Schallfrequenz von 110 kHz kaum weiter als 8 m gehört werden können, denn die Amplitude der Schallwellen ist nach 8 m auf nur ca. 3% reduziert verglichen mit Wellen im menschlichen Audiobereich, die auf diese Entfernung keine merkbare Dämpfung erfahren.
Bei größeren Entfernungen zwischen Schallquelle und Schallempfänger wird die Frequenz-abhängige Dämpfung auch für das menschliche Ohr sehr deutlich, etwa bei OpenAir-Veranstaltungen: Nach einigen Kilometern Schallweg ist von der Musik nur noch der tiefe Bass übrig.
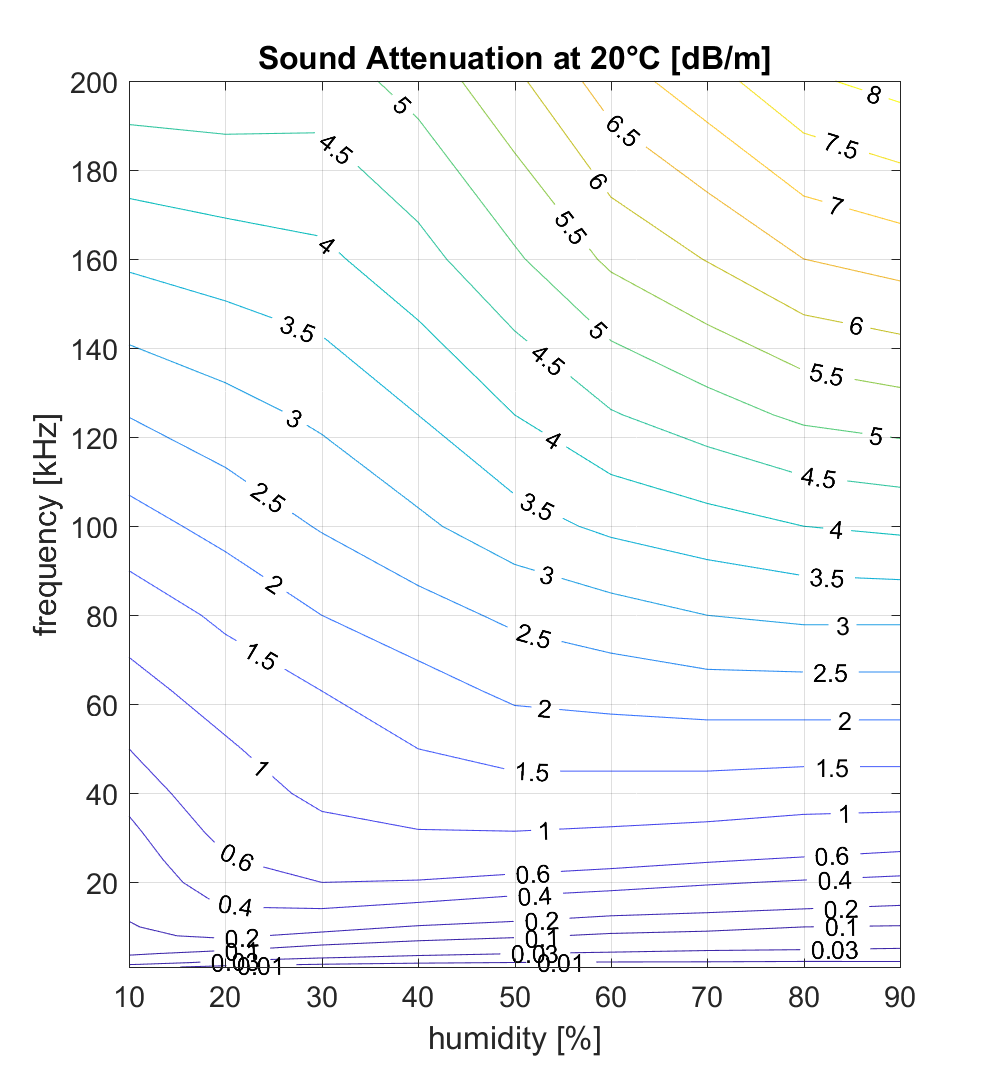
Die Abhängigkeit der Schalldämpfung von Temperatur und Luftfeuchte ist ziemlich kompliziert. Dies zeigt die folgende Graphik, die die Dämpfung in dB/m angibt.
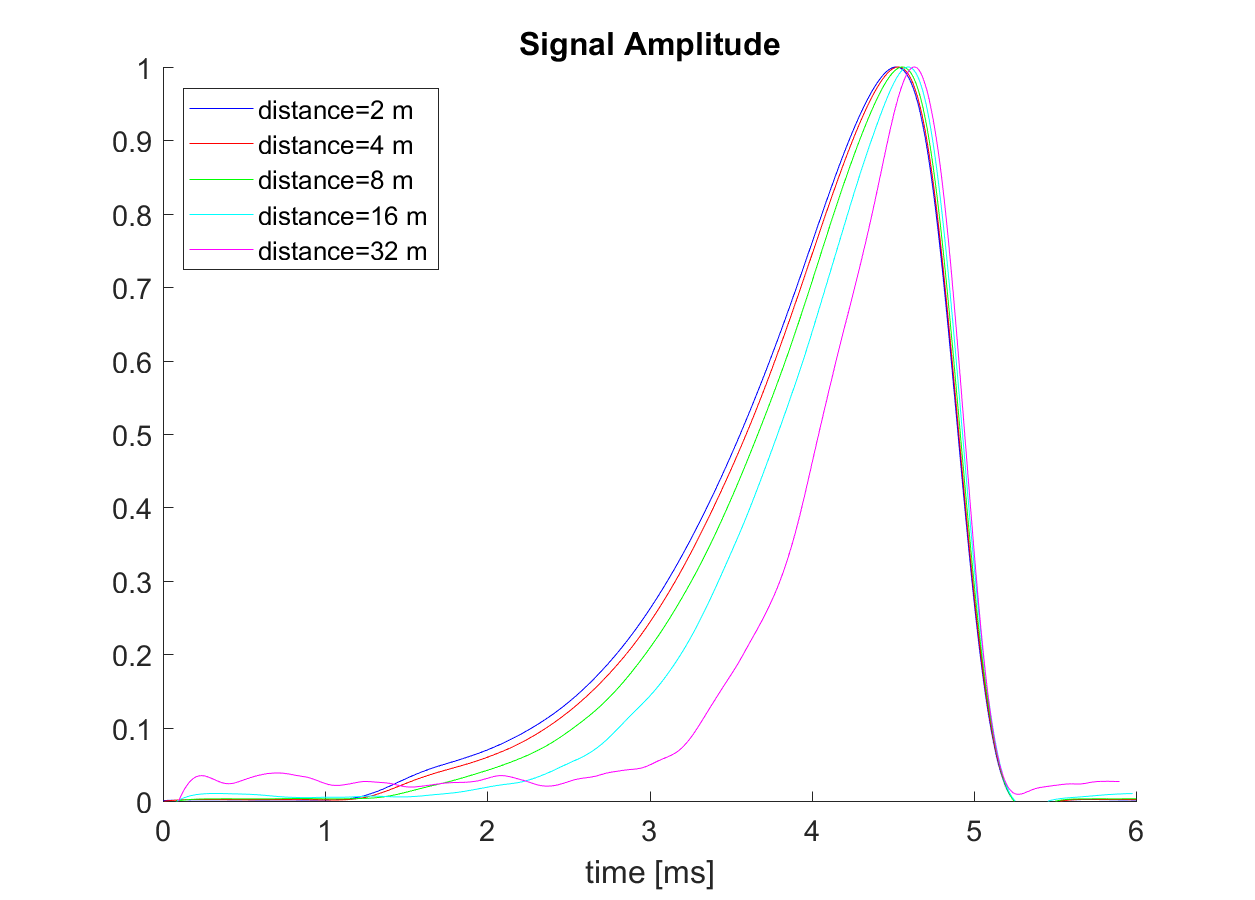
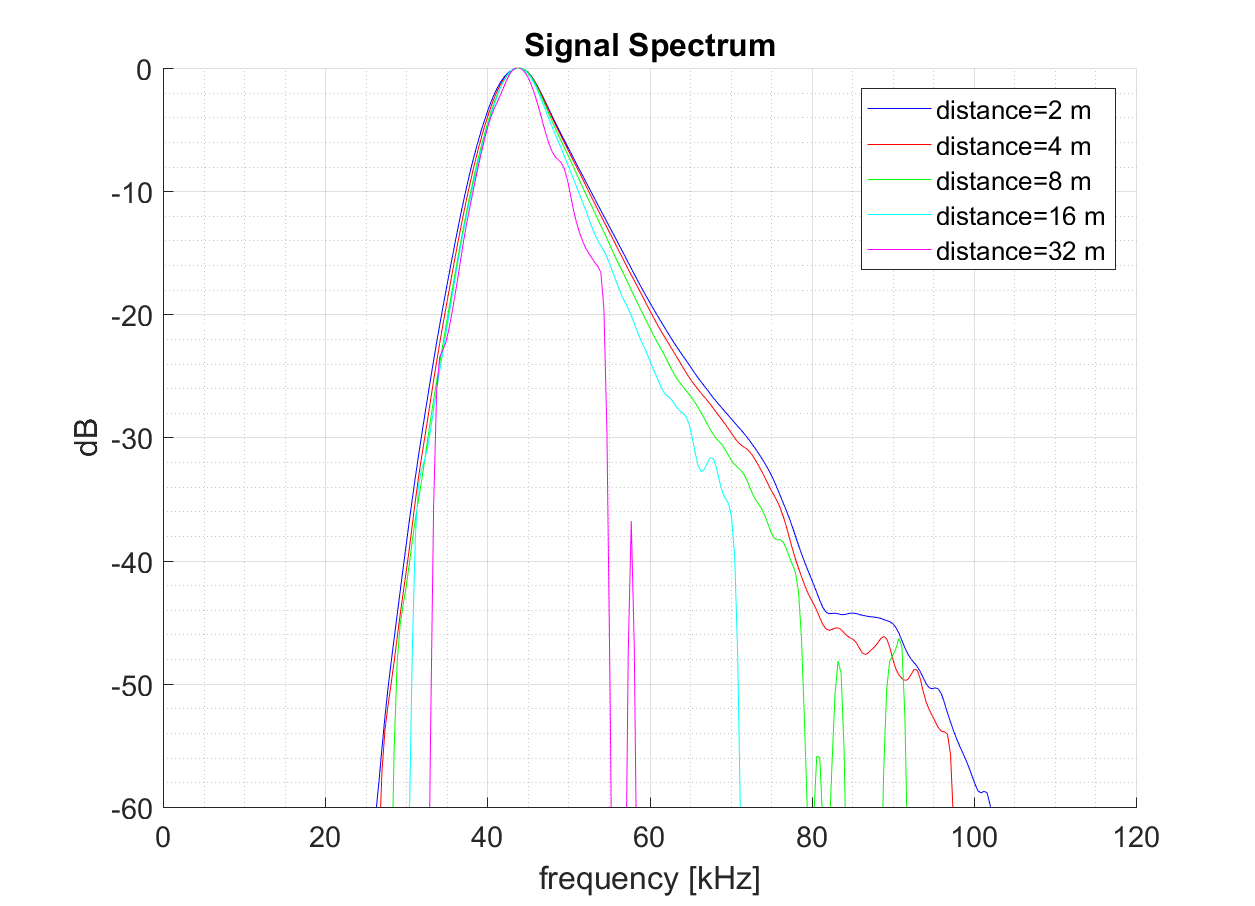
Da die Dämpfung von der Frequenz stark abhängt, können Fledermausrufe, die einen größeren Frequenzbereich überstreichen, durch die Dämpfung verändert werden. Als Beispiel dient hier ein simulierter Ortungsruf der Wasserfledermaus. Nachfolgend ist die Veränderung des Rufprofils und des Spektrums zu sehen. Der Ruf wird mit zunehmender Entfernung kürzer, die Startfrequenz sinkt, die Endfrequenz steigt etwas, aber die Hauptfrequenz bleibt (fast) unverändert:
Beugung
Wenn in der Nähe des Schallausbreitungsweges
Hindernisse existieren, findet eine Beugung der Schallwellen statt, durch
die die Wellen sich auch um Hindernisse herum ausbreiten. Diese
Ausbreitung ist abhängig von der Wellenlänge λ =
c /
f , wo c
= 340 m/s die Schallgeschwindigkeit und f
die Frequenz der
Schallschwingung bedeuten.
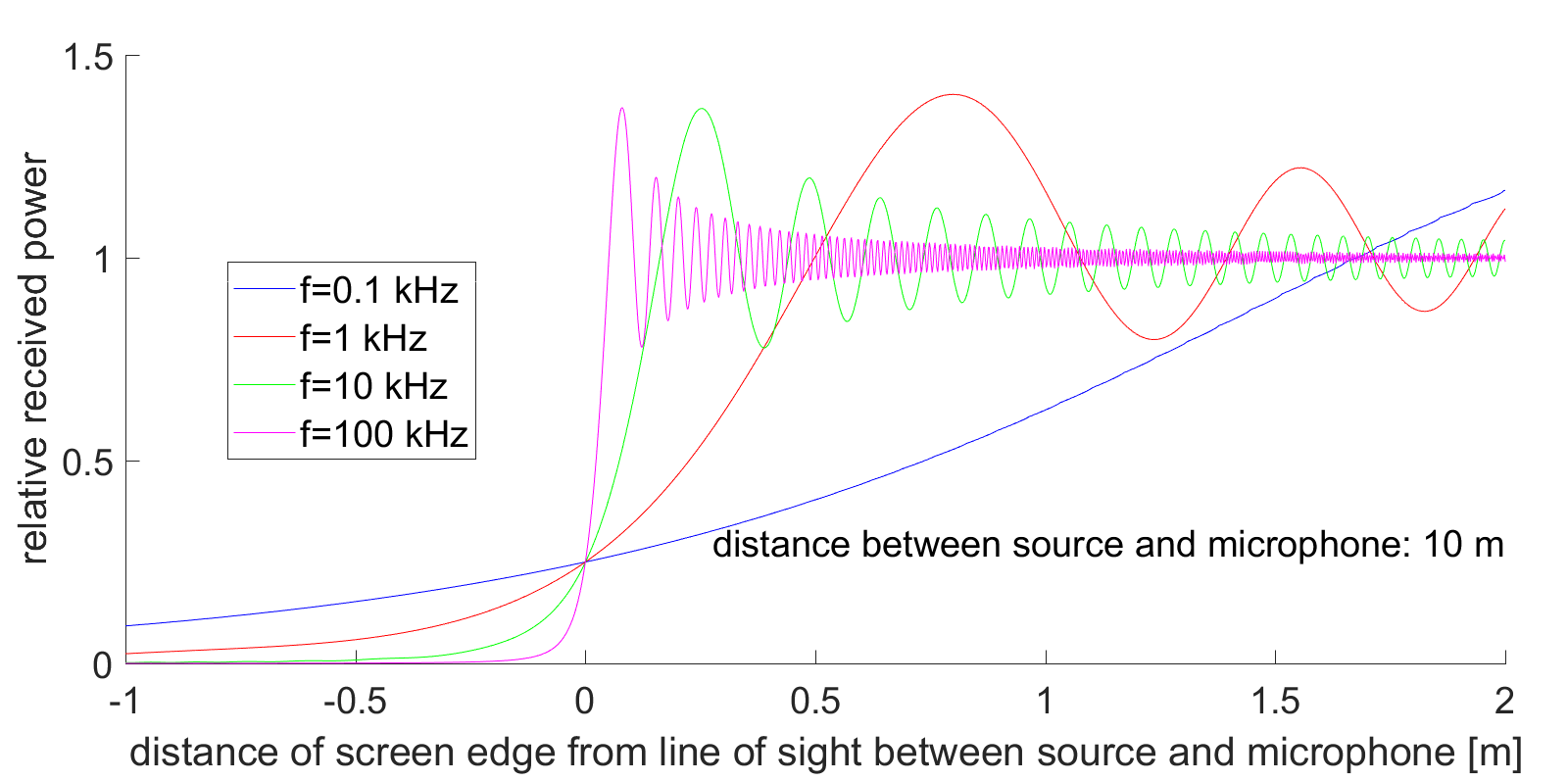
Die folgende Illustration nimmt einen unendlich großen Raum an, in dem sich Schallwellen ungehindert zwischen einer Quelle und einem 10 m entfernten Mikrofon ausbreiten können. Nun schiebt man eine schallabsorbierende Wand zwischen Quelle und Mikrofon. Das Bild zeigt die vom Mikrofon gemessene Schwingungsamplitude in Abhängigkeit von der Distanz der Wandkante vom direkten Strahl zwischen Quelle und Mikrofon, und dies für vier Frequenzen als Parameter. Hier zeigt sich dass die Wand auch bei der tiefen Frequenz von 100 Hz sehr wohl stört. Aber es gibt keinen klaren Schallschatten. Das ändert sich bei höheren Frequenzen: Eine Hufeisennase, die hinter einem Baumstamm ruft, kann man nicht hören, weil der Stamm einen Schallschatten wirft mit einer ziemlich scharfen Grenze fast wie bei Lichtwellen.